Making exams add up: the effects of aggregation
By Neil Stringer
Published 12 Dec 2013
GCSEs and A-levels normally involve more than one examination, partly because of the amount of material to be examined, and partly because it makes sense to examine particular parts of a subject separately. For example, in modern foreign languages, reading and writing are often assessed separately from listening and speaking. This helps candidates know what to expect from each paper, and makes things simpler for the examiners who write, mark, and set grade boundaries on the papers.
However, any exam with multiple papers also involves a little-noticed but important stage, known as aggregation. A candidate's final grade in a subject is based on his or her combined results in all the papers, and aggregation is the process of combining them. It is at the aggregate level that the results are used and standards are maintained. But standards which are set at the paper level do not always translate to satisfactory outcomes at subject level. The complexities of aggregation can affect the initial setting of standards, the year-on-year maintenance of standards, and the maintenance of standards when the examination model is changed.
Consider the three subjects represented in the diagram. Each is examined via three papers. The coloured circles show the number of candidates getting an A in each paper. Candidates who achieve an A on all three papers achieve an A overall. In each subject, exactly the same number of candidates achieve grade A on each of the three papers, so all the circles are the same size. But the overlap between the candidates who achieve an A on each paper varies between the subjects: from high in the first example, lower in the second, to lower still in the third. This means that despite similar outcomes on the papers, the subject outcomes overall differ widely.
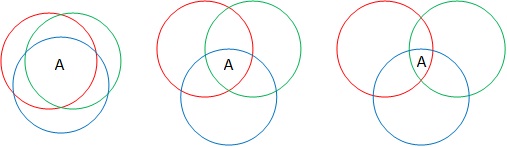
This happens because most subjects are multi-faceted, but some are more multi-faceted than others. The less alike the content of each paper is, the less likely it is that any candidate will score similarly on each paper. The first subject could consist of fairly homogenous content divided into three papers; the third could be three distinct skills. So it is far easier to be an all-rounder in subject one than in subject three. Traditionally, exam boards have used two methods to address such aggregation issues. In the case of linear exams those in which all of the candidates in a cohort must sit the exact same exam paper at the same time one option is to calculate the mean percentage of candidates achieving (in this example) a grade A across the papers and reduce the total number of marks needed for an A to the mark that produces that same percentage at subject level.
In the example below, there are three papers with different grade boundaries and percentages of candidates achieving grade A. When the grade A boundaries are simply summed, the boundary for the whole assessment is 215 marks and the percentage of candidates achieving it is 7%. By contrast, the percentile method matches the average outcome across the papers 13% at subject level by adjusting the aggregate boundary downwards.
| Grade A Boundary | % Achieving Grade A | |
| Paper 1 | 70 | 12% |
| Paper 2 | 65 | 9% |
| Paper 3 | 80 | 18% |
| Subject Aggregate (Addition Method) | 215 | 7% |
| Subject Aggregate (Percentile Method) | 207 | 13% |
In the case of modular exams in which candidates within a cohort may sit different versions of exam papers at different times the percentile method is not usable. Instead, to change the number of As awarded at subject level, the number of As awarded at paper level must change. This method can also be used for linear exams.
In the example of our three subjects, decreasing the number of As awarded for subject one requires us to raise the grade boundaries and so reduce the number of As achieved on the papers. Increasing the number of As awarded for subject three requires us to lower the grade boundaries and so increase the number of As achieved on the papers. This effectively makes the coloured circles smaller and larger, respectively, but ensures that the overlap areas are closer in size.
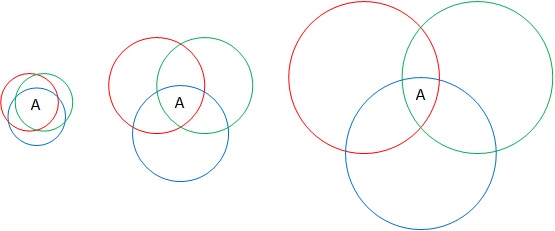
Any syllabus may exhibit year-on-year fluctuations in the consistency of candidates' performances across the papers. This could happen because certain topic pairings draw on slightly more common knowledge, skills, or understanding than others. This will result in slight changes in the subject standards unless they are adjusted. Because GCSE and A-level standards are maintained at subject level, paper boundaries sometimes move more or less than we might expect from the difficulty of the individual papers, because the way the papers aggregate has changed.
The argument for maintaining standards at subject level is most compelling when specifications are redeveloped. Something as simple as changing the number of papers constituting the assessment can affect how the papers aggregate. A fairly recent example of this was the move from 6-unit A-levels to 4-unit A-levels. By modelling the relationship between the units in the 6-unit specifications, we were able to determine the change in unit-level standards needed in the 4-unit specifications to produce a comparable set of outcomes at subject level. The effect of changing the number of units depends on how consistently candidates perform across papers, and this varies between subjects. It would be difficult to justify candidates suddenly obtaining higher grades in a given subject simply because the content had been rearranged across a different number of papers, especially if the effect applied only to certain subjects.
This is a simplification: in practice, obtaining a mark above the A boundary on one unit can compensate for obtaining a mark below the A boundary on another unit. Nonetheless, the principle is the same: the number of As at subject level depends on the overlap between the candidates scoring highly on each paper.
Neil Stringer
Keywords
Related content
- Are my exams harder than yours?
- There’s more to accessibility than extra time
- Do tests help you learn?
About our blog
Discover more about the work our researchers are doing to help improve and develop our assessments, expertise and resources.
Share this page
Connect with us
Email: research@aqa.org.uk
Work with us to advance education and enable students and teachers to reach their potential.